Yapılması gereken işleri yapmak
için kas kuvvetine ihtiyaç duyarız. Ancak bazı işleri yaparken kaslarımız
yetersiz kalır. Bu durumda basit makinelerden yararlanırız. Günlük hayatımızda
kullandığımız kaldıraç, eğik düzlem, makara, dişli, çark, vida gibi birçok
basit makineler vardır.
Kuvvetin yönünü ve büyüklüğünü değiştiren
makinelere basit makine denir. Basit
makine yardımı ile büyük ağırlıktaki malzemeleri daha küçük kuvvetle hareket
ettirebiliriz.

Basit makineler;
Ø Enerji
üretmezler.
Ø İş
kolaylığı sağlarlar.
Ø İşten
kazanç yoktur.
Ø Kuvvetten
kazanç varsa yoldan kayıp vardır.
Ø Yoldan
kazanç sağlanabilir.
Ø Yoldan
kazanç varsa kuvvetten kayıp vardır.
Ø Kuvvetin
yönü değiştirilebilir.
1. F = P veya P / F = 1 ise; kuvvet ve yoldan kazanç ya da kayıp yoktur.
1. F = P veya P / F = 1 ise; kuvvet ve yoldan kazanç ya da kayıp yoktur.
( Kuvvet Kazancı
= 1 )
2.
F
> P veya P / F < 1 ise; kuvvetten kayıp, yoldan kazanç vardır.
( Kuvvet Kazancı
< 1 )
3.
F
< P veya P / F > 1ise; kuvvetten kazanç, yoldan kayıp vardır.
( Kuvvet Kazancı
> 1 )
A.
KALDIRAÇLAR
Destek üzerinde rahatça hareket eden çubuklara kaldıraç denir. Kaldıraçlarda
kuvvetin destek noktasına olan uzaklığına kuvvet
kolu, yükün destek noktasına olan uzaklığına ise yük kolu denir.
Kaldıraçlar da işlem yapılırken;
Kuvvet
( F ) . Kuvvet Kolu ( x ) = Yük ( P ) . Yük
Kolu ( y )
Kuvvet Kazancı = P / F veya x
/ y
Kaldıraçların
özellikleri farklılık gösterebilir.
a.
Desteğin Kuvvet İle Yük Arasında
Olduğu Kaldıraçlar
Bu kaldıraçlarda destek noktası
ortadadır. Bu kaldıraçlara örnek olarak, tahterevalli, pense, kriko, makas,
kerpeten…
ÖRNEK 1 - Aşağıdaki kaldıracın dengeye
gelebilmesi için uygulanması gereken kuvveti ve kuvvet kazancını bulunuz.
ÇÖZÜM:
KUVVET.
KUVVET KOLU = YÜK. YÜK KOLU
F . 4 = 60 . 2
F = 30 N
KUVVET KAZANCI = YÜK / KUVVET
KUVVET KAZANCI = 60 / 30
KUVVET KAZANCI = 2 ‘dir.
( P > F; Olduğu için kuvvetten
kazanç, yoldan kayıp vardır.)
ÖRNEK 2 - Aşağıdaki kaldıracın dengede olduğuna
göre cismin ağırlığını ve kuvvet kazancını bulunuz.
ÇÖZÜM:
KUVVET.
KUVVET KOLU = YÜK. YÜK KOLU
8 . 5 = P . 1
P = 40 N
KUVVET KAZANCI = YÜK / KUVVET
KUVVET KAZANCI = 40 / 8
KUVVET KAZANCI = 5 ‘dir.
( P > F; Olduğu için kuvvetten
kazanç, yoldan kayıp vardır. )
ÖRNEK 3 - Aşağıdaki kaldıracın dengeye
gelebilmesi için uygulanması gereken kuvveti ve kuvvet kazancını bulunuz.
ÇÖZÜM:
KUVVET.
KUVVET KOLU = YÜK. YÜK KOLU
F . 3 = 30 . 3
F = 30 N
KUVVET
KAZANCI = YÜK / KUVVET
KUVVET KAZANCI = 30 / 30
KUVVET KAZANCI = 1 ‘dir.
ÇÖZÜM:
KUVVET
KAZANCI = YÜK / KUVVET veya KUVVET KOLU / YÜK KOLU
KUVVET
KAZANCI = KUVVET KOLU / YÜK KOLU
KUVVET KAZANCI = 3 / 4 = 0,75
( Kuvvet Kazancı < 1 olduğu için
kuvvetten kayıp, yoldan kazanç vardır. )
b.
Yükün Destek ile Kuvvet Arasında
Olduğu Kaldıraçlar
Bu kaldıraçların destek noktası uç
kısımdadır. Bu kaldıraçlara örnek olarak, el arabası, gazoz açacağı, ceviz
kıracağı, kürek, kapı…
Bu tür kaldıraçlarda her zaman kuvvet kolu,
yük kolundan büyük olacağı için, her zaman kuvvetten kazanç, yoldan kayıp
vardır.
ÖRNEK 1 – Aşağıdaki kaldıracın dengeye
gelebilmesi için uygulanması gereken kuvveti ve kuvvet kazancını bulunuz.
ÇÖZÜM:
KUVVET.
KUVVET KOLU = YÜK. YÜK KOLU
F . 6 = 28 . 3
F = 14 N
KUVVET KAZANCI = YÜK / KUVVET
KUVVET
KAZANCI = 28 / 14
KUVVET KAZANCI = 2 ‘dir.
( P > F; Olduğu için kuvvetten
kazanç, yoldan kayıp vardır. )
ÖRNEK 2 – Aşağıdaki kaldıracın dengede olduğu
biliniyor ise kuvvet kazancı kaçtır?
ÇÖZÜM:
KUVVET
KAZANCI = YÜK / KUVVET veya KUVVET KOLU / YÜK KOLU
KUVVET
KAZANCI = KUVVET KOLU / YÜK KOLU
KUVVET KAZANCI = 7 / 5 = 1,4
( Kuvvet Kazancı > 1 olduğu için
kuvvetten kazanç, yoldan kayıp vardır. )
c.
Kuvvetin Yük ile Destek Arasında
Olduğu Kaldıraçlar
Bu
kaldıraçların destek noktası uç kısımdadır. Bu kaldıraçlara örnek olarak,
cımbız, olta, maşa, tel zımba aleti, insan kolu…
Bu tür kaldıraçlarda her zaman kuvvet
kolu, yük kolundan küçük olacağı için, her zaman kuvvetten kayıp, yoldan kazanç
vardır.
ÖRNEK 1 - Aşağıdaki kaldıracın dengede olduğu
biliniyor ise kuvvet kazancı kaçtır?
ÇÖZÜM:
KUVVET
KAZANCI = YÜK / KUVVET veya KUVVET KOLU / YÜK KOLU
KUVVET KAZANCI = KUVVET KOLU / YÜK KOLU
KUVVET KAZANCI = 1 / 6 = 0,16
(
Kuvvet Kazancı < 1 olduğu için kuvvetten kayıp, yoldan kazanç vardır. )
B.
MAKARALAR
Ağır bir cismi yükseğe kaldırmak için çoğu zaman makara sisteminden
yararlanılır. İnşaat ve fabrikalarda küçük kuvvetle çok ağır yükler
taşınabilmektedir. Kullanılan makara sayısına ve çeşidine göre 3 çeşit yapıları
vardır.
1. Sabit
Makara
Merkezinden sabitlenen makaralardır. Ağır bir cismi yükseğe kaldırmak
için kullanılır. Kuvvetten kazanç sağlamaz. Ancak kuvvetin yönünü değiştirdiği
için yükün taşınması kolaylaşır. Kuvvet ile ağırlık zıt yönde hareket eder.
Sabit makaralar da uygulanan kuvvet ile yükün ağırlığı aynı olduğu için
kuvvetten ve yoldan kazanç veya kayıp yoktur. Sadece kuvvetin yönü farklıdır.
Kuvvet = Yük
Kuvvet Kazancı = Yük / Kuvvet = 1
olduğu için kuvvetten kazanç veya kayıp yoktur.
Sabit makaralarda ip ne kadar çekilirse yük de o kadar yukarı çıkar.
Sabit makara sadece iş yapma kolaylığı sağlar.
ÖRNEK 1 – Aşağıdaki makara sistemi dengede olduğuna göre
kuvvet kaç Newton dur ve kuvvet kazancı hakkında bilgi veriniz.
ÇÖZÜM:
Şekildeki
sabit makaradır. Sabit makaralarda;
F
= P olduğu için
F =10 N
Kuvvet
Kazancı = P / F = 10 /10 = 1
Kuvvet Kazancı = 1 olduğu için kuvvet
kazancı yoktur.
Kuvvet
Kazancı olmadığı için yoldan da kazanç yada kayıp yoktur.
2.
Hareketli Makara
İpin sabitlenerek makaradan geçtiği makaralardır. Bu makaralarda yük
makaraya asılır. İpin serbest ucuna kuvvet uygulanarak yük taşınır. Yük ile
aynı yönde makarada taşınır. Yük kuvvet ile aynı yönde hareket eder.
2 x Kuvvet = Yük
Hareketli makaralarda kuvvet kazanç ve
yoldan kayıp vardır.
Hareketli makarada ip 2m yukarı çekilirse
yük 1m yükselir.
Yandaki hareketli makara örneğinde 2 kat
kuvvet kazancı varken, 2 kat da yoldan kayıp vardır.
Hareketli makaralarda yükün büyüklüğü
kuvvetten fazladır.
( P = 2F )
Kuvvet Kazancı = P / F >1 olduğu için
kuvvet kazancı vardır.
Not: Makara ağırlığı verilirse, makara
ağırlığı yük ile toplanır.
ÖRNEK
1 – Aşağıdaki makara sistemi dengede
olduğuna göre kuvvet kaç Newton dur ve kuvvet kazancı hakkında bilgi veriniz.

ÇÖZÜM:
Şekildeki
makara hareketli makaradır. Hareketli makaralarda;
P
= 2F
12
= 2F
F = 6 N
Kuvvet
Kazancı = P / F = 12 / 6 = 2
Kuvvet
Kazancı = 2 olduğu için kuvvetten kazanç, yoldan kayıp vardır.
3.
Palangalar
Sabit makara ile hareketli makaradan
oluşan birleşik makara sistemine palanga denir. Palangalarda kuvvet kazancı
sağlanırken kuvvetin yönü de değiştirilebilir. Palangalarda sabit makara ile
hareketli makara arasındaki ip sayısı arttıkça uygulanacak kuvvetin değeri
azalır. Yani kuvvet kazancı artar.
Not:
Palangalarda
her zaman kuvvet kazancı ve yoldan kayıp vardır.
Birleşik Palangalarda kuvvet bulunurken şunlara dikkat
edilmelidir;
1.
Palangada
Kuvvet Aşağı Yönlü İse;
F = Yük / Makara Sayısı
F= 30 / 2
F = 15 N
2.
Palangalarda Kuvvet Yukarı Yönlü İse;
F = Yük /
(Makara Sayısı + 1 )
F = 60 / (2 +1)
F = 60 / 3
F
= 20 N
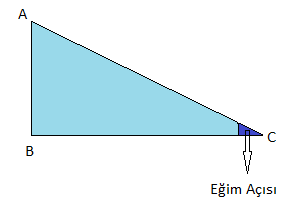
C.
EĞİK DÜZLEM
Küçük kuvvet ile
ağır yükleri istenilen yüksekliğe çıkarmak için oluşturulan yokuşlara eğik düzlem
denir. Eğik düzlem basit makineler arasında en
kolay olanıdır. Bir kamyona eşya yüklerken kamyonun
kasasına yatay bir tahta
konulur ve iterek eşyalar kamyona çıkarılır. İtme kuvveti her zaman yükün
ağırlığından küçüktür.
F: Uygulanan Kuvvet
h: Yükün Aldığı Yol ( Yük Kolu )
L: Kuvvetin Aldığı Yol ( Kuvvet Kolu )et
Yük x Yük
Kolu = Kuvvet x Kuvvet Kolu
P . h = F. L
Eğik düzlemde her zaman kuvvetten kazanç, yoldan kayıp
vardır.
Eğik düzlemler
de;
v Kuvvetin büyüklüğü
artar.
v Kuvvet
kazancı azalır.
v Yol kaybı
azalır.
Not: “h” artarsa kuvvet artar, kuvvet kazancı azalır. “L”
artarsa kuvvet kazancı artar.
ÖRNEK
1 - P Yükünün ağırlığı 25 N
olduğuna göre F kuvveti kaç N’dir?
P . h
= F . L
25 . 1,2 = F . 3
30 = 3 F
F= 10 N
D.
ÇIKRIK
Dönme eksenleri aynı ve yarıçapları
farklı olan 2 silindirin üst üste yerleştirilmesi sonucu oluşmuştur. Bu basit
makinelere el mikseri, kalemtıraş, kıyma makinesi, bisiklet pedalı, kuyu suyu
sistemi örnek verilebilir.
Çıkrıklarda kuvvet her zaman yükten küçük
olduğu için, çıkrıklarda kuvvetten kazanç vardır.
Çıkrıklarda aşağıdaki eşitlik
yazılabilir.






























Teşekkür ederiz öğretmenim.
YanıtlaSilTebrikler
YanıtlaSilBu yorum bir blog yöneticisi tarafından silindi.
YanıtlaSilgüzel yararlı...
YanıtlaSilonur hocam çok iyi..
YanıtlaSilNFK dan selamlar
teşekkürler
YanıtlaSil